Indefinite Integration of the Gamma Integral
and Related Statistical Applications
2.3 The Nature of the Unsolved Puzzle:
Invalid Asymptotic Analysis
Since r \in \left( 0,1 \right), we can assume r={q}/{p}, where 0<q<p, and derive an identity expression of
\Gamma \left( -r+1 \right)
\begin{equation*}
\Gamma \left( -r+1 \right)=\frac{p}{p-q}\int_{0}^{\infty }{{\exp(-{{x}^{\frac{p}{p-q}}})}dx}. \tag{2.13}
\end{equation*}
[Proof for (2.13)]
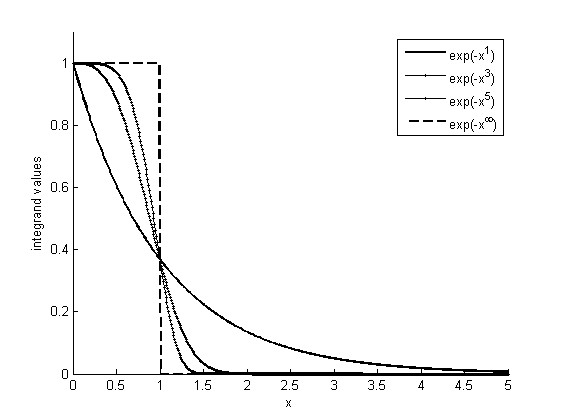
Figure 1: Functional Plots of \exp \left( -{{x}^{p/\left( p-q \right)}} \right)
Plotting the integrand function \exp \left( -{{x}^{p/\left( p-q \right)}} \right) as Figure 1 shows, we know that the error is trivial for calculating the gamma function by replacing the upper limit \infty with a considerably larger
number, noted as "C" herefater. Consider the case that has the largest error, where {p}/{\left( p-q \right)\to 1}, the errors can be evaluated by
\begin{equation*}
\int_{C}^{\infty }{{\exp(-x)}dx=-{\exp(-C)}}.
\end{equation*}
The result indicates the errors are -2.06e-09, -1.93e-22, and -3.72e-44 for C=20, 50, and 100, respectively. Given (2.12), we can always evaluate the gamma function with arbitary precision by employing the "h" factorization method.
For computational purposes, we need to set a proper value for C without causing a significant error when evaluating the gamma function. Doing so helps us understand the algebraic properties of the "h" function. As (2.10) shows, the core of the "h" function, \underset{n\to \infty }{\mathop{\lim }}\,\sum\limits_{i=0}^{n}{{{w}_{i}}{{\beta }_{i}}}, is a monotonically decreasing series, that is composed of two sets of parameters: {{w}_{i}} and {{\beta }_{i}}. The former serves as a weighting factor, the ratio of the gamma integral with an upper limit c to the same integral with an infinite upper limit. The latter is a function of ith order forward difference, starting from 1/\left( 1-r \right) and ending at 1/\left( i+1-r \right). The upper limit c is supposed to approach infinity, as is the number of expansion terms n.
The value of the weighting factor {{w}_{i}} is bounded within the interval \left( 0,1 \right) and can be expressed as follows:
\begin{equation}
{{w}_{i}}=\frac{\int_{0}^{c}{{{x}^{i}}{\exp(-x)}dx}}{\int_{0}^{\infty }{{{x}^{i}}{\exp(-x)}dx}}.
\tag{2.14}
\end{equation}
[Proof for (2.14)]
Theoretically, c should be set as \infty , which makes all {{w}_{i}} become one. Meanwhile, as the number of
expansion terms n increases, the value of the difference function will approach a limit determined by \Gamma \left( 1-r \right) and
{{n}^{-\left( 1-r \right)}}.
\begin{align*}
\underset{n\to \infty }{\mathop{\lim }}\,{{\beta }_{n}}&=\underset{n\to \infty }{\mathop{\lim }}\,\frac{n!}{\left( 1-r \right)
\left( 2-r \right)\cdots \left( n+1-r \right)} \\ \notag
&\to \frac{\Gamma \left( 1-r \right)}{{{n}^{1-r}}} \tag{2.15}.
\end{align*}
[Proof for (2.15)]
Notice that {{\beta }_{i}} is monotonically decreasing to the convergence value,
\begin{equation*}
{{\beta }_{0}}>{{\beta }_{1}}>\cdots >{{\beta }_{n}}\to \frac{\Gamma \left( 1-r \right)}{{{n}^{1-r}}} \tag{2.16}
\end{equation*}
[Proof for (2.16)]
and thus, the sum of the infinite series \underset{n\to \infty }{
\mathop{\lim }}\,\sum\limits_{i=0}^{n}{{{w}_{i}}{{\beta }_{i}}} will approach infinity
\begin{equation}
\underset{n\to \infty }{\mathop{\lim }}\,\,\sum\limits_{i=1}^{n}{{{w}_{i}}{{\beta }_{i}}}>
\underset{n\to \infty }{\mathop{\lim }}\,\frac{n\Gamma \left( 1-r \right)}{{{n}^{1-r}}} \to \infty .
\tag{2.17}
\end{equation}
[Proof for (2.17)]
This result obviously deviates from our conclusion as shown in the Proof for
(2.11)
\begin{equation*}
\underset{n\to \infty }{\mathop{\lim }}\,\sum\limits_{i=0}^{n}{{{w}_{i}}{{\beta }_{i}}} =-{{c}^{r}}\Gamma \left( -r \right)-\frac{1}{r}.
\end{equation*}
The two conflicting results make clear that the nature of the problem is related to the invalid asymptotic analysis when we treat the upper limit of the gamma integral as infinity.
